The Beta-Binomial Model
Dr. Dogucu
Posterior for the Beta-Binomial Model
Let π∼Beta(α,β) and X|n∼Bin(n,π).
Posterior for the Beta-Binomial Model
Let π∼Beta(α,β) and X|n∼Bin(n,π).
f(π|x)∝Γ(α+β)Γ(α)Γ(β)πα−1(1−π)β−1(nx)πx(1−π)n−x
Posterior for the Beta-Binomial Model
Let π∼Beta(α,β) and X|n∼Bin(n,π).
f(π|x)∝Γ(α+β)Γ(α)Γ(β)πα−1(1−π)β−1(nx)πx(1−π)n−x
f(π|x)∝π(α+x)−1(1−π)(β+n−x)−1
Posterior for the Beta-Binomial Model
Let π∼Beta(α,β) and X|n∼Bin(n,π).
f(π|x)∝Γ(α+β)Γ(α)Γ(β)πα−1(1−π)β−1(nx)πx(1−π)n−x
f(π|x)∝π(α+x)−1(1−π)(β+n−x)−1
π|x∼Beta(α+x,β+n−x)
Posterior for the Beta-Binomial Model
Let π∼Beta(α,β) and X|n∼Bin(n,π).
f(π|x)∝Γ(α+β)Γ(α)Γ(β)πα−1(1−π)β−1(nx)πx(1−π)n−x
f(π|x)∝π(α+x)−1(1−π)(β+n−x)−1
π|x∼Beta(α+x,β+n−x)
f(π|x)=Γ(α+β+n)Γ(α+x)Γ(β+n−x)π(α+x)−1(1−π)(β+n−x)−1
Conjugate prior
We say that f(π) is a conjugate prior for L(π|x) if the posterior, f(π|x)∝f(π)L(π|x), is from the same model family as the prior.
Thus, Beta distribution is a conjugate prior for the Binomial likelihood model since the posterior also follows a Beta distribution.
Bike ownership
The transportation office at our school wants to know π the proportion of people who own bikes on campus so that they can build bike racks accordingly. The staff at the office think that the π is more likely to be somewhere 0.05 to 0.25. The plot below shows their prior distribution. Write out a reasonable f(π). Calculate the prior expected value, mode, and variance.
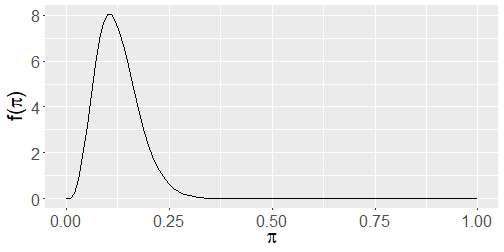
Plotting the prior
plot_beta(5, 35)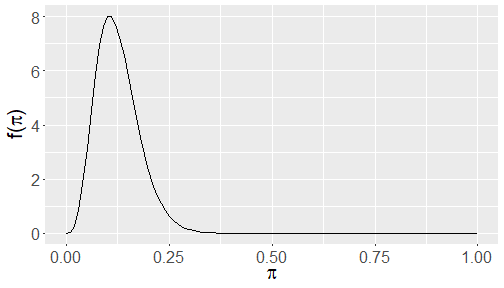
Summarizing the prior
summarize_beta(5, 35)## mean mode var## 1 0.125 0.1052632 0.002667683Bike ownership posterior
The transportation office decides to collect some data and samples 50 people on campus and asks them whether they own a bike or not. It turns out that 25 of them do! What is the posterior distribution of π after having observed this data?
Bike ownership posterior
The transportation office decides to collect some data and samples 50 people on campus and asks them whether they own a bike or not. It turns out that 25 of them do! What is the posterior distribution of π after having observed this data?
π|x∼Beta(α+x,β+n−x)
Bike ownership posterior
The transportation office decides to collect some data and samples 50 people on campus and asks them whether they own a bike or not. It turns out that 25 of them do! What is the posterior distribution of π after having observed this data?
π|x∼Beta(α+x,β+n−x)
π|x∼Beta(5+25,35+50−25)
Bike ownership posterior
The transportation office decides to collect some data and samples 50 people on campus and asks them whether they own a bike or not. It turns out that 25 of them do! What is the posterior distribution of π after having observed this data?
π|x∼Beta(α+x,β+n−x)
π|x∼Beta(5+25,35+50−25)
π|x∼Beta(30,60)
Plotting the posterior
plot_beta(30, 60)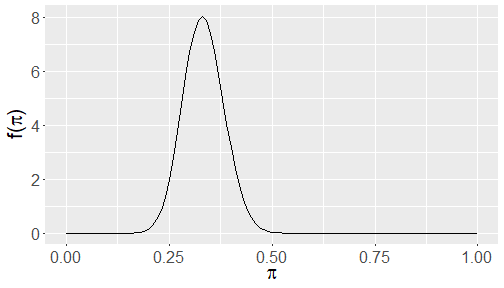
Summarizing the posterior
summarize_beta(30,60)## mean mode var## 1 0.3333333 0.3295455 0.002442002Plot summary
plot_beta(30, 60, mean = TRUE, mode = TRUE)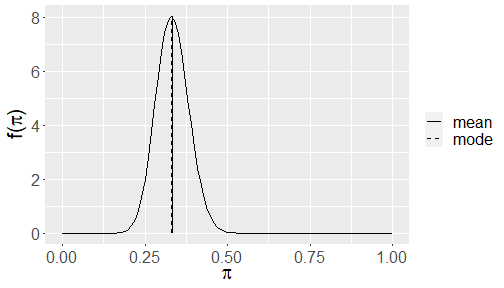
Bike ownership: balancing act
plot_beta_binomial(alpha = 5, beta = 35, x = 25, n = 50)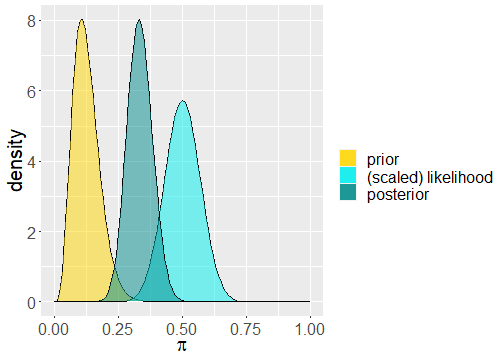
Posterior Descriptives
π|(X=x)∼Beta(α+x,β+n−x)
E(π|(X=x))=α+xα+β+n Mode(π|(X=x))=α+x−1α+β+n−2 Var(π|(X=x))=(α+x)(β+n−x)(α+β+n)2(α+β+n+1)
Bike ownership - descriptives of the posterior
What is the descriptive measures (expected value, mode, and variance) of the posterior distribution for the bike ownership example?
Bike ownership - descriptives of the posterior
What is the descriptive measures (expected value, mode, and variance) of the posterior distribution for the bike ownership example?
summarize_beta_binomial(5, 35, x = 25, n = 50)## model alpha beta mean mode var## 1 prior 5 35 0.1250000 0.1052632 0.002667683## 2 posterior 30 60 0.3333333 0.3295455 0.002442002